قضیه حد مرکزی چیست؟ سفری به دل نظم در میان تصادفها
تصور کن یک سکهی معمولی در دست داری. آن را چند بار به هوا میاندازی. یکبار میشود شیر، دو بار خط. دفعهی بعد شاید پنجبار پشتسرهم خط بیاید. انگار هیچ قاعدهای در کار نیست. همهچیز تصادفی است.
اما حالا فرض کن همین سکه را هزار بار بیندازی. اتفاق جالبی رخ میدهد. دیگر آن بینظمیهای اولیه به چشم نمیآیند. به احتمال زیاد، چیزی نزدیک به پانصد بار شیر میآید و پانصد بار خط. نه همیشه دقیق، اما چنان نزدیک که حس میکنی نظمی پنهان در کار است.
حالا یک قدم جلوتر برو. تصور کن هزاران نفر دیگر همین آزمایش را انجام دهند. اگر بخواهیم نتایجشان را روی نموداری رسم کنیم، شکلی آشنا پدیدار میشود. شکلی که انگار آن را بارها در جاهای مختلف دیدهایم: یک منحنی زنگولهای با قلهای درست در وسط، همانجا که میانگین قرار دارد.
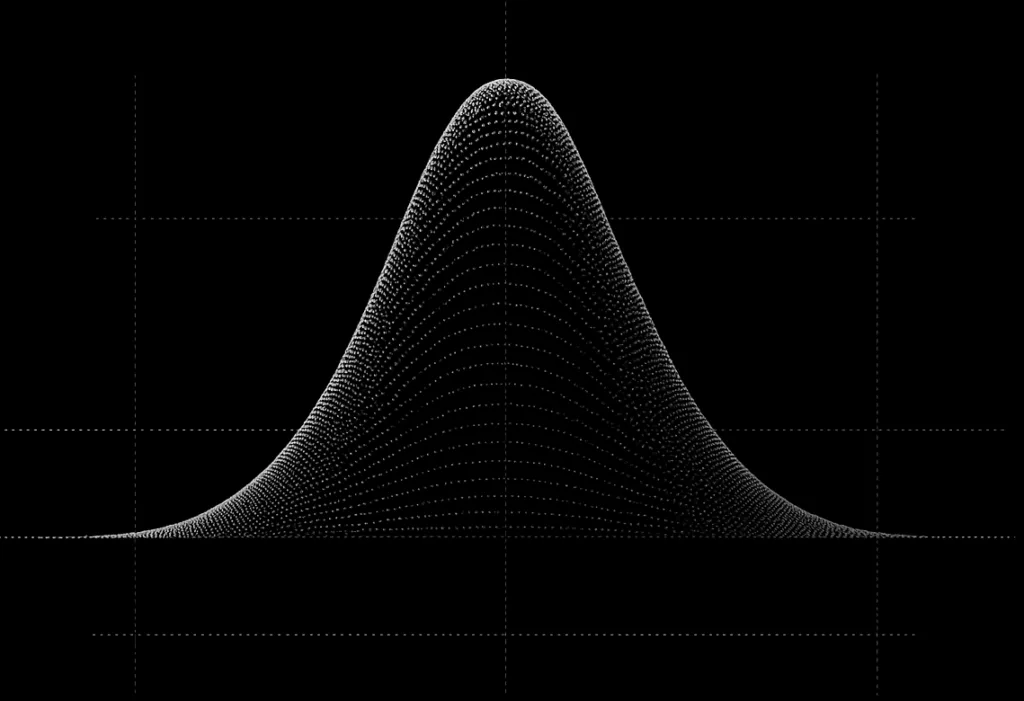
و اینجاست که یکباره سؤال بزرگی مطرح میشود:
چطور ممکن است از دل آشوب و تصادف، چنین نظم خیرهکنندهای بیرون بیاید؟
چرا رفتار بیقاعدهی پرتاب سکه، در مجموع، به الگویی مشخص و قابل پیشبینی تبدیل میشود؟
آیا این فقط یک توهم آماری است یا حقیقتی عمیقتر در دل طبیعت؟
اگر کنجکاو هستید بدانید قضیه حد مرکزی چیست و چرا این نظم پنهان در دادههای تصادفی ظاهر میشود، پاسخ این راز را ریاضیدانها بعد از دو قرن تلاش پیدا کردند. نامش شاید در ابتدا خشک و علمی بهنظر برسد، اما در دل خود بینشی انسانی و فلسفی دارد: قضیهی حد مرکزی (Zentraler Grenzwertsatz).
ایدهای که میگوید اگر با دقت کافی به مجموعهای از دادههای پراکنده و تصادفی نگاه کنیم، در نهایت، الگویی منظم و قابل پیشبینی در دل آنها پدیدار خواهد شد.
همهچیز از یک سکه شروع شد
داستان از قرن هجدهم آغاز میشود. دورانی پرهیاهو در تاریخ علم؛ زمانی که اروپا به جوش و خروش افتاده بود، آزمایشگاهها در حال گسترش بودند و ذهنهای بزرگ میخواستند جهان را با عدد و فرمول توضیح دهند. این همان دورهای بود که دانشمندان باور داشتند اگر دقیقتر اندازهگیری کنند، شاید بتوانند حتی آینده را هم پیشبینی کنند.
در همین فضای پر امید، مردی زندگی میکرد به نام آبراهام دو موآور (Abraham de Moivre)، ریاضیدانی فرانسوی که بهخاطر باورهای مذهبیاش از فرانسه رانده شده بود و پناه به انگلستان برده بود. مردی تبعیدی، اما با ذهنی آرامناپذیر.
او که عاشق الگوها بود، ساعتهای زیادی را صرف بررسی بازیهایی مانند پرتاب سکه میکرد. و در همین بازی ساده بود که متوجه چیزی عجیب شد:
اگر تعداد پرتابهای سکه زیاد باشد، نتایج آن دیگر آنقدرها هم بیقاعده به نظر نمیرسند. انگار الگوی خاصی در حال شکلگیری است. انگار آشوب، دارد به نظم میل میکند.
برای آن زمان، این فقط یک مشاهدهی تجربی بود. نه اثباتی داشت و نه نامی علمی. حتی کسی آن را جدی نمیگرفت. اما همین مشاهدهی ساده، مثل جرقهای خاموش، آغاز سفری شد که بیش از دو قرن طول کشید. سفری از دل سکههای شیر و خط، به قلب ریاضیات مدرن.
از تصادف تا قانون: وقتی ریاضی بهدنبال نظم میگردد
با گذشت زمان، آن جرقهی خاموشی که دو موآور روشن کرده بود، آرامآرام ذهنهای دیگر را هم درگیر کرد. در پایان قرن هجدهم، نوبت به یکی از بزرگترین متفکران فرانسه رسید: پیر-سیمون لاپلاس (Pierre-Simon Laplace).
او مردی بود با اعتقادی راسخ به نظم جهانی. در نگاه لاپلاس، اگر انسانی میتوانست موقعیت و سرعت تمام ذرات جهان را در یک لحظه بداند، میتوانست آینده را با دقتی بینقص پیشبینی کند. حتی شانس، از نظر او، فقط نامی دیگر برای نادانی ما بود.
با همین دیدگاه، لاپلاس سراغ ایدهی دو موآور رفت. او تلاش کرد آن را گسترش دهد، دقیقترش کند، و به آن ساختاری ریاضی ببخشد. کارش را با توزیعهای دوجملهای شروع کرد، اما هدفش چیزی فراتر بود: پیدا کردن قانونی که نشان دهد چرا آشوب، در مقیاس بزرگ، به تعادل میرسد.
سؤالی که ذهنش را مشغول کرده بود، هرچند خودش آن را اینگونه بیان نکرد، دقیقاً همان چیزی بود که ما امروز با عنوان «قضیه حد مرکزی» میشناسیم.
اما هنوز چیزی کم بود. ایدهی شکلگیری نظم از دل تصادف، بیشتر شبیه یک «حدس زیبا» بود تا یک قانون ریاضی اثباتشده. چیزی در حد یک شهود فلسفی، نه یک قضیهی قابل اتکا برای دانشمندان.
و سرانجام، آنچه را که ذهنهای فرانسوی آغاز کرده بودند، قرار بود ریاضیدانانی در شرق اروپا به پایان برسانند. روسیه وارد ماجرا شد و با خود، انضباطی تازه و رویکردی تازهتر به مفاهیم احتمال آورد.
روسیه، سرزمین نظم در دل بینظمی
در قرن نوزدهم، جایی دور از هیاهوی پاریس و لندن، در سرزمینی سرد و پهناور، موجی آرام اما پرقدرت در حال شکلگیری بود. روسیه که تا آن زمان در ریاضیات اروپا نقشی کمرنگتر داشت، ناگهان به یکی از قطبهای اصلی تفکر آماری تبدیل شد.
یکی از نخستین ستارههای این آسمان تازه، پافنوتی چبیشف (Pafnuti Tschebyschev) بود. مردی سختکوش و دقیق که باور داشت باید از دل دادهها، قانون بیرون کشید. او نخستین کسی بود که تلاش کرد نشان دهد چرا وقتی دادههای تصادفی زیاد میشوند، رفتارشان به میانگین ثابتی میل میکند. چرا وقتی مجموعهی بزرگتری از چیزهای غیرقابل پیشبینی داشته باشی، تصویر کلیات قابل پیشبینیتر میشود.
اما چبیشف فقط آغاز ماجرا بود. شاگرد او، مردی آرام با چهرهای همیشه نگران و چشمانی مشتاق به نام الکساندر لیاپونوف (Aleksandr Ljapunov)، مأموریت ناتمام استادش را ادامه داد.
در سال ۱۹۰۱، لیاپونوف با روشی نوآورانه توانست اثبات کند که اگر تعداد زیادی دادهی تصادفی و مستقل را با هم جمع بزنیم، بدون آنکه شکل توزیع اولیهشان مهم باشد، نتیجه همیشه به یک توزیع خاص میل میکند. همان زنگولهی آشنای ما؛ پاسخی ابتدایی به پرسشی که بعدها در قالب نظریهای مشهور و بنیادی در آمار مطرح شد، یعنی اینکه قضیه حد مرکزی چیست و چرا چنین الگویی شکل میگیرد.
اما هنوز یک قطعهی دیگر باقی مانده بود. کمی بعد، ریاضیدان دیگری به نام آندری مارکوف (Andrei Markow) پا به میدان گذاشت. او نهتنها مسیر لیاپونوف را ادامه داد، بلکه آن را گستردهتر کرد. مارکوف نشان داد که حتی اگر دادهها از جنسهای مختلف باشند، بهشرط آنکه وابسته بههم نباشند، باز هم همان الگوی آشنا ظاهر میشود.
در آن روزها، آنچه دانشمندان روسی ساخته بودند، تنها یک نظریهی آماری نبود. آنها داشتند به جهان نشان میدادند که حتی از دل بینظمی محض، میتوان قانون بیرون کشید.
آلمان و زنگولهای که ریاضی را متحول کرد
فرانسویها ایده را کاشتند. روسها آن را پروراندند. اما شاید این آلمان بود که آن را به بنای اصلی ریاضیات مدرن تبدیل کرد.
در قرن نوزدهم، در میان تپههای سبز گوتینگن و تالارهای خاموش دانشگاههای پروس، مردی زندگی میکرد که بهاندازهی یک عصر تأثیرگذار بود: کارل فریدریش گاوس (Carl Friedrich Gauß). ریاضیدانی آلمانی با ذهنی چنان دقیق که هنوز هم به او لقب «شاهزادهی ریاضیات» میدهند.
گاوس در تلاش برای درک خطاهای اندازهگیری در نجوم، به شکلی خاص از توزیع دادهها رسید: نموداری که قلهای در وسط دارد و دو طرفش بهتدریج افت میکند، همان منحنی زنگولهای معروف. فرم ریاضی این منحنی را او نوشت؛ منحنیای که امروز آن را به نام خودش میشناسیم: توزیع نرمال گاوسی (Normalverteilung nach Gauß).
شاید گاوس خودش نمیدانست که این منحنی بعدها تبدیل به امضای جهان شود. از نتایج آزمایشهای پزشکی گرفته تا تحلیل بازارهای مالی، از پیشبینیهای آبوهوا تا دادههای روانشناسی، همه جا پای آن زنگوله در میان است.
اما آلمان فقط محل تولد شکل ریاضی این تابع نبود؛ محل طرح پرسش های هم بود. در قرن بیستم، چهرههایی چون ریشارد فن میزس (Richard von Mises) و هانس رایشنباخ (Hans Reichenbach) پا به میدان گذاشتند. آنها میپرسیدند:
اصلاً احتمال چیست؟ آیا چیزی واقعی است؟ یا فقط راهی برای کنار آمدن با نادانی ماست؟
آیا آماری که در مقیاس بزرگ نظم نشان میدهد، واقعاً بازتاب طبیعت است؟ یا فقط توهمی جمعی، حاصل نگاه ما به شلوغی دنیا؟
پرسشهایی که نهتنها به قلب فلسفهی علم رفتند، بلکه هنوز هم برای ما زندهاند. پاسخشان بسته به این است که چطور به جهان نگاه کنیم: آیا جهان قانونمند است و ما باید کشفش کنیم؟ یا این ما هستیم که برای آرام کردن ذهنمان، به هرجومرج بیرونی، نظم میدهیم؟ و اگر نظم واقعاً وجود دارد، پس قضیه حد مرکزی چیست جز تلاشی برای دیدن تصویر کلی در دل آشفتگی؟
شاید همانطور که گاوس نشان داد، نظم وجود دارد، اما دیدنش نیاز به زاویهی درست دارد.
دیدگاه جالب شارل دو گل، رئیسجمهور فرانسه درباره نام آوران و دانشمندان آلمانی
کولموگوروف: کسی که قطعات پازل را کنار هم چید
تا اینجا، داستان ما پر بود از ایدههایی الهامبخش، مشاهداتی تجربی، و تلاشهایی برای نظم دادن به آشوب. اما هنوز یک چیز کم بود: پایهای محکم که بتوان بر آن ایستاد. قانونی ریاضی، نه شهودی؛ قابل اعتماد، نه فقط احتمالی.
در دههی ۱۹۲۰، مردی جوان از روسیه وارد صحنه شد که سرنوشت این داستان را تغییر داد. نامش آندری کولموگوروف (Andrei Kolmogorow) بود. چهرهای آرام، اما ذهنی بیوقفه در حرکت. او نهفقط ریاضیدان، که معمار نوعی جدید از تفکر بود.
کولموگوروف کاری کرد که هیچکس پیش از او نکرده بود: او نظریهی احتمال را از دنیای حدس و گمان بیرون کشید و آن را به یک نظام کامل و قابل اتکا تبدیل کرد. تا پیش از او، قضیهی حد مرکزی بیشتر شبیه یک قانون نانوشته بود. اگر آزمایش را زیاد تکرار کنی، نظم پیدا میشود… البته شاید! اما کولموگوروف نشان داد که اگر شرایط مشخصی برقرار باشد، دیگر «شاید» در کار نیست. آن نظم، قطعی است. دقیق است. و مانند ساعت، همیشه کار میکند.
او برای احتمال، همان کاری را کرد که نیوتن برای فیزیک کرد: نظم را به جایی برد که پیشتر فقط شهود بود.
کولموگوروف فقط فرمول نمینوشت. او داشت زبان آشوب را به زبان منطق ترجمه میکرد. ریاضیات برایش فقط ابزار نبود؛ نوعی نگاه به جهان بود، جهانی که هرچند پر از تصادف و نوسان است، اما اگر درست نگاه کنی، قوانین خودش را دارد.
نگاهی از بالا: وقتی بینظمی معنا پیدا میکند
قضیهی حد مرکزی فقط یک فرمول نیست. مثل پنجرهای است که از آن میتوان به دنیای واقعی نگاه کرد.
وقتی درگیر جزئیات باشیم، همهچیز پراکنده و بینظم به نظر میرسد. هر تصمیم، هر رفتار، هر اتفاق انگار تصادفی و بیقاعده است. مثل آدمهایی که در خیابانی شلوغ راه میروند، بیهدف، بیجهت.
اما کافیست چند قدم عقب برویم. از بالا نگاه کنیم. آنوقت متوجه میشویم که همان آشفتگی، شکل دارد. همان شلوغی، الگو دارد. آدمها در مجموع، جهت دارند. جامعه مثل رودخانهای است که اگرچه قطرههایش پرآشوباند، مسیرش روشن است.
قضیهی حد مرکزی همین را میگوید:
اگر بهجای غرق شدن در دادههای تکی، به کلیت نگاه کنیم، نظم خودش را نشان میدهد.
اگر از دل آشوب، اطلاعات را بیرون بکشیم و صبور باشیم، حقیقت خودش را آشکار میکند.
این فقط درس آمار نیست. درسی است برای زندگی. اینکه به جای ترسیدن از بینظمی، باید فرصت بدهیم تا تصویر کلی خودش را کامل کند. و آنگاه، شاید بفهمیم که حتی تصادف هم بیدلیل نیست.
در پایان: صدایی آرام در دل شلوغیها
دنیا پر از صداست. خبرها، اتفاقها، بحرانها… هر لحظه چیزی تازه از راه میرسد، توجهمان را میگیرد و آرامشمان را بر هم میزند. انگار جایی برای فهم عمیق باقی نمانده است. اما در دل همین شلوغی، قضیهای هست که میگوید: اگر صبور باشی، اگر درست نگاه کنی، اگر میان دادهها و اتفاقهای پراکنده، دنبال تصویر کلی بگردی، حقیقت را خواهی دید.
در جامعهای مثل ایران، که گاهی حس میشود هر کس مسیر خودش را میرود و آشوب از هر طرف بالا گرفته، شاید سخت باشد دیدن تصویر کلی. اما اگر از دل جزئیات گذر کنیم، اگر مجموعهی رفتارها را ببینیم، اگر آنچه را تکرار میشود با دقت دنبال کنیم، شاید بتوان نشانههایی از جهت آینده را دید.
قضیهی حد مرکزی، در نهایت، به ما یادآوری میکند که حتی در جهانی پر از تصادف، الگو هست. و اگر یاد بگیریم چگونه ببینیمش، شاید زندگی هم کمی قابلفهمتر شود.
اگر به دنبال درک بهتر مفهوم این قضیه هستید، پیشنهاد میکنیم ویدئو توضیح علمی اصول قضیه حد مرکزی که به دقت و با جزئیات زیاد از منظر علم ریاضی بررسی می کند را مشاهد کنید.





































نظر خود را به اشتراک بگذارید